
A package for the numerical solution of systems of polynomial equations.
Applications
Kinematic synthesis
The problem of finding all four-bar linkages whose coupler curve passes through nine prescribed points has been a longstanding unsolved problem in kinematics until it got solved by Wampler, Morgan and Sommese in 1992. While this has been an outstanding computational achievement at the time we now can synthesis the mechanism from scratch in a matter of minutes using HomotopyContinuation.jl.
Topological Data Analysis
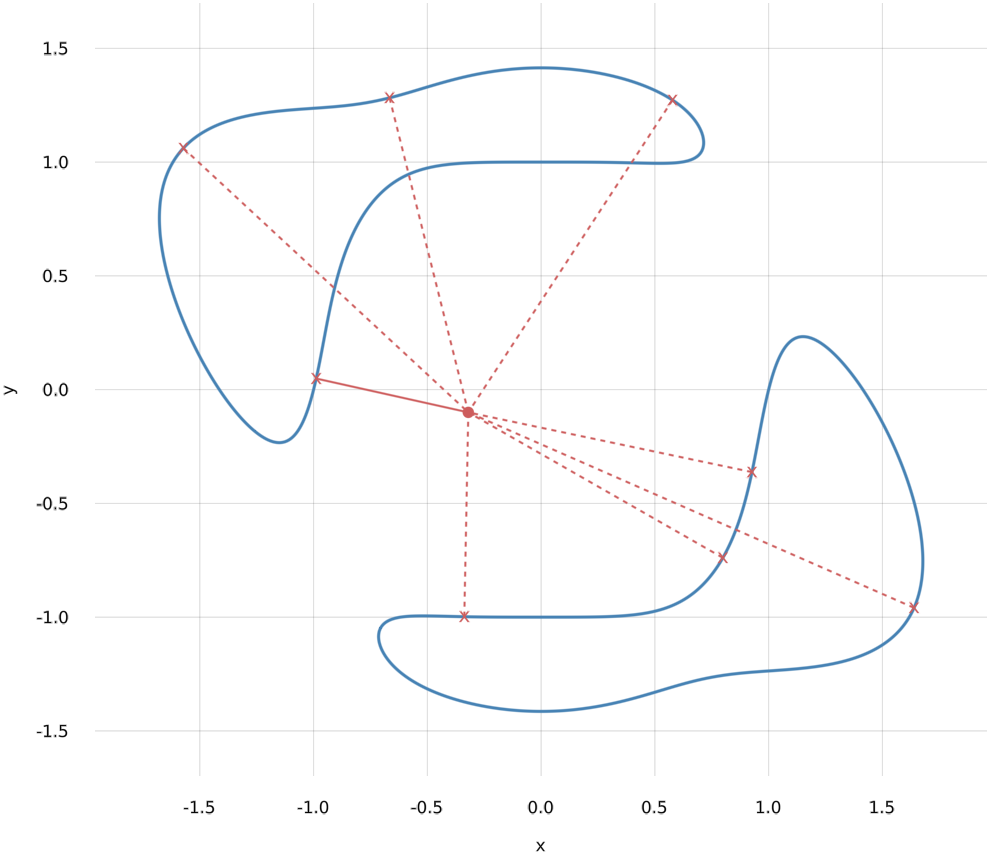
The geometry of bottlenecks plays an important role in several important aspects of real geometry in connection with analysis of data with support on an algebraic variety $X$. Together with the maximal curvature of the variety they define the reach of $X$. Knowing the reach allows to compute the correct homology of an variety. Using HomotopyContinuation.jl we can compute the reach for curves and surfaces.
Computational Chemistry
Homotopy continuation methods allow us to study the conformation space of molecules as for example cyclooctane (CH₂)₈. It consists of eight carbon atoms aligned in a ring, and eight hydrogen atoms, each of which is attached to one of the carbon atoms. It is known that the conformation space is homeomorphic to a union of the Klein bottle and a sphere, which intersect in two rings. Follow our example to find out how to sample from this conformation space.
Constrained Optimization
Many models in the sciences and engineering are expressed as sets of real solutions to systems
of polynomial equations. We can optimize any objective whose gradient is an algebraic function using homotopy methods
by computing