A complex sextic curve in $\mathbb{C}^3$ is the intersection of a cubic surface $\mathcal{C}\subset \mathbb{C}^3$ with a quadric $\mathcal{Q}\subset \mathbb{C}^3$; that is, there exist polynomials in three variables $C$ of degree 3 and $Q$ of degree 2, such that $\mathcal{C} = \{x\in\mathbb{C}^3 : C(x) = 0\}$ and $\mathcal{Q} = \{x\in\mathbb{C}^3 : Q(x) = 0\}$.
An interesting fact about such sextic curves is that they have 120 complex tritangents (at least almost all of them). This means that there are 120 affine complex planes, that touch the sextic at three points.
For instance, the sextic with $Q=x_3 - x_1x_2$ and $C=x_1^3+x_2^3+x_3^3 - 1$ together with one of its tritangents is shown below ($C$ is called the Fermat cubic). The tangent plane is depicted as a triangle. The red points are the points at which the plane touches the sextic.
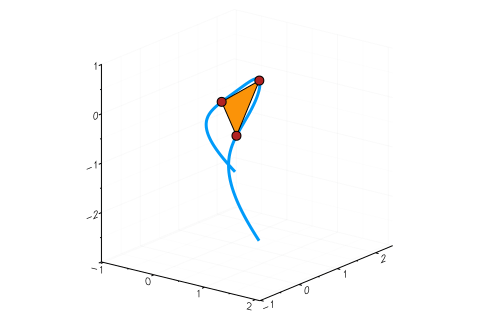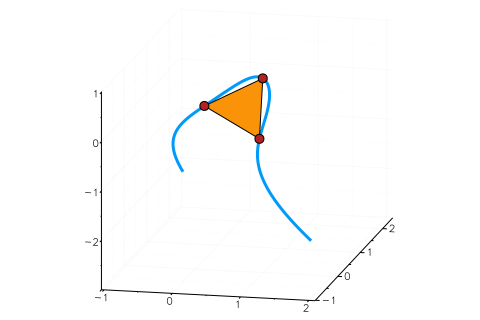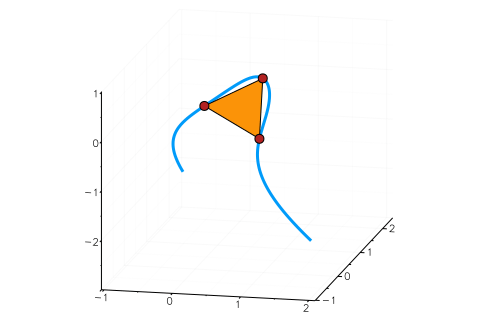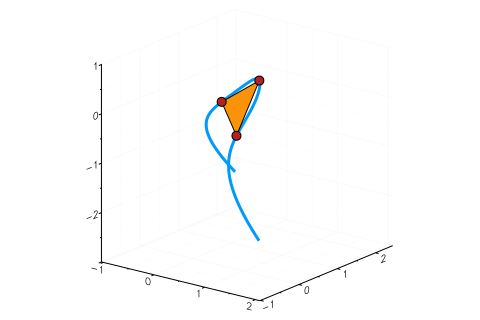
In the last months, tritangents have been a popular research topic in the Nonlinear Algebra Group at MPI Leipzig: Türkü Özlüm Celik, Avinash Kulkarni, Yue Ren, Mahsa Sayyary Namin, Emre Sertöz and Bernd Sturmfels have worked on this and wrote several articles, which you can find here, here and here.
Computing tritangents numerically is the topic of this blog post. I want to follow the strategy proposed by Hauenstein et. al., who discuss how to compute tritangents using Bertini. I will repeat their computations using HomotopyContinuation.jl.
Let $\mathcal{V} = \mathcal{C}\cap \mathcal{Q}$ be a sextic in $\mathbb{C}^3$ and let $H\subset \mathbb{C}^3$ be an affine plane. Being a tritangent means that there exists three points $x,y,z\in \mathcal{V}$ with
$$x \in H, \mathrm{T}_x \mathcal{V} \subset H, \text{ and } y \in H, \mathrm{T}_y \mathcal{V} \subset H, \text{ and } z \in H, \mathrm{T}_z \mathcal{V} \subset H.$$
The points $x,y,z$ are the contact points of the plane $H$ with $\mathcal{V}$.
Let $h\in \mathbb{C}^3$ be a vector with $H=\{x\in \mathbb{C}^3: h^Tx=1\}$. Then, $H$ is a tritangent with contact points $x,y,z$, if and only if $(x,y,z,h)$ is a zero of the following polynomial system:
$$ F = \begin{bmatrix} P(x,h) \\ P(y,h)\\ P(z,h)\end{bmatrix}, \text{ where } P(x,h) = \begin{bmatrix} h^T x - 1 \\ Q(x) \\ C(x) \\ \det([h \nabla_xQ \nabla_xC]) \end{bmatrix}.$$
Here, $\nabla_x$ denotes the gradient operator. Let us create the system $F$ in Julia. For simplicity, I will consider the case when $Q=x_3 - x_1x_2$.
using HomotopyContinuation, LinearAlgebra
@var h[1:3] # variables for the plane
@var x[1:3] y[1:3] z[1:3] #variables for the contact points
#the quadric
Q = x[3] - x[1] * x[2]
#the cubic C with coefficients c
C, c = dense_poly(x, 3, coeff_name = :c)
#generate the system P for the contact point x
P_x = [
h ⋅ x - 1;
Q;
C;
det([h differentiate(Q, x) differentiate(C, x)])
]
#generate a copy of P for the other contact points y,z
P_y = [p([h; x; c] => [h; y; c]) for p in P_x]
P_z = [p([h; x; c] => [h; z; c]) for p in P_x]
#define F
F = System([P_x; P_y; P_z]; variables = [h;x;y;z], parameters = c)
Let us first solve F by total degree homotopy when the coefficients of C are random complex numbers.
#create random complex coefficients for C
c₁ = randn(ComplexF64, 20)
#solve the system for c₁
S = solve(F; target_parameters = c)
On my laptop the computation takes 14 seconds. Here is what I get.
Result with 4020 solutions
==========================
• 12636 paths tracked
• 720 non-singular solutions (0 real)
• 3300 singular solutions (0 real)
• random_seed: 0x825eefa1
• start_system: :polyhedral
• multiplicity table of singular solutions:
┌───────┬───────┬────────┬────────────┐
│ mult. │ total │ # real │ # non-real │
├───────┼───────┼────────┼────────────┤
│ 1 │ 2499 │ 0 │ 2499 │
│ 2 │ 131 │ 0 │ 131 │
│ 3 │ 670 │ 0 │ 670 │
└───────┴───────┴────────┴────────────┘
The count of 720 is correct: for each of the 120 tritangents I get 6 solutions corresponding to all permutations of the contact points $x,y,z$ — and $6 \cdot 120 = 720$.
Let us extract the 720 solutions.
sols = solutions(S)
One may use sols in a parameter homotopy for computing the tritangents of other sextics. Here is code for tracking sols from c₁ to $x_1^3+x_2^3+x_3^3-1$.
#define the coefficients for C
c₀ = coeffs_as_dense_poly(x[1]^3+x[2]^3+x[3]^3-1, x, 3)
#track the solutions from c₁ to c₀
R = solve(F, sols, start_parameters = c₁, target_parameters = c₀)
On my laptop this computation takes 0.048781 seconds — tracking solutions from c₁ to c₀ is much faster than using the direct solve approach. Here is the summary of R:
Result with 684 solutions
=========================
• 720 paths tracked
• 684 non-singular solutions (24 real)
• random_seed: 0x2bae05f8
From the $4= \frac{24}{6}$ real solutions one was used in the gif above.
Cite this example:
@Misc{ tritangents2025 ,
author = { Paul Breiding },
title = { Tritangents },
howpublished = { \url{ https://www.JuliaHomotopyContinuation.org/examples/tritangents/ } },
note = { Accessed: May 5, 2025 }
}