The article Random points on an algebraic manifold proposes an algorithm for sampling from probability distributions on a variety based on linear slicing. In this example, we want to apply this algorithm to sample from the plane curve
$$V = \{ x=(x_1,x_2) \in \mathbb{R}^2 \mid x_1^4+x_2^4-3x_1^2-x_1x_2^2-x_2+1=0\}.$$
intersected with the box $B = [-2,2]\times [-2,2]$.
Suppose that $f:V\to \mathbb{R}_+$ is a measurable function. We want to sample from the density $f(x)/(\int_{V} f(x) \mathrm{d}V)$. We will consider the example $f(x)=1$, which gives the uniform distribution on $V\cap B$. For the algorithm we need upper bounds
$$K\geq \sup \{ f(x) \mid x\in V\cap B\} \quad \text{and}\quad C\geq \sup \{\Vert x\Vert^2 \mid x\in V\cap B\}.$$ We take $K = 1$ and $C = 8$.
The algorithm goes as follows. Intersect $V\cap B$ with a random line $L={a_1x+a_2y=b}$, where $a_1,a_2$ and $b$ are independent standard Gaussian random variables. Then, compute the following sum:
$$\overline{f}(a_1,a_2,b) := \sum_{x\in V\cap B\cap L} \frac{f(x)}{\alpha(x)}, \text{ where } \alpha(x)= \frac{1}{\pi} \frac{\sqrt{1+ \langle x,\pi_x x\rangle}}{1+\Vert x\Vert^2},$$
where $\pi_x$ is the orthogonal projection onto the normal space of $V$ at $x$. Because $d=\mathrm{deg}(V)=4$ has degree $4$, there are at most 4 points in the section $ V\cap B\cap L$, and so
$$p:= \frac{\overline{f}(a_1,a_2,b)}{w} \leq 1, \text{ where } w=dK(1+C).$$
Then, we throw a biased coin $Z$ with $\mathrm{Prob}\{Z=1\} = p$.
- If $Z=1$, we choose $x\in V\cap B\cap L$ with probability $\frac{f(x) \alpha(x)}{\overline{f}(a_1,a_2,b)}$.
- If $Z=0$, we reject the sample.
This procedure produces points from the density $f(x)/(\int_V f(x)\mathrm{d}x)$.
Let us sample in Julia. First, we set up the equations
using HomotopyContinuation, LinearAlgebra, Distributions
@polyvar x[1:2]
F = x[1]^4+x[2]^4-3x[1]^2-x[1]*x[2]^2-x[2]+1
J = differentiate(F, x)
K, C, d = 1, 8, 4
w = d * K * (1+C)
and we define $\alpha(x)$.
function α(z, J)
N = normalize!([j(x=>z) for j in J])
sqrt(1 + (z ⋅ N)^2) / (1 + z⋅z) / pi
end
Now, we define a function that implements the rejection sampling.
f(x) = 1.0 # so that we sample the uniform distribution
function rejection_step(R)
if nreal(R) > 0
S = real_solutions(R)
# intersect M ∩ L with the box B
filter!(s -> abs(s[1]) < 2 && abs(s[2]) < 2, S)
if !isempty(S)
β = map(z -> f(z) / α(z, J), S)
f̄ = sum(β)
p = f̄ / w
# rejection step
if rand(Bernoulli(p)) == 1
p = β ./ f̄
i = rand(Categorical(p))
return S[i]
end
end
end
# return Inf if sample was rejected
return fill(Inf,2)
end
We create a suitable start system by intersecting $V$ with a random complex linear space.
@polyvar a[1:2] b
G = [F; a⋅x - b]
a₀, b₀ = randn(ComplexF64, 2), randn(ComplexF64)
start = solve([subs(g, a=>a₀, b=>b₀) for g in G])
start_sols = solutions(start)
Now, we track start_sols to various random real intersections, following this guide. In the code below we make $k=10^2$ trials to get points.
k = 10^2
#track towards k random linear spaces
points = solve(
G,
start_sols;
parameters = [a; b],
start_parameters = [a₀; b₀],
target_parameters = [randn(3) for _ in 1:k],
transform_result = (R,p) -> rejection_step(R)
)
filter!(p -> !(Inf in p), points)
The points we get from executing this code are shown next.
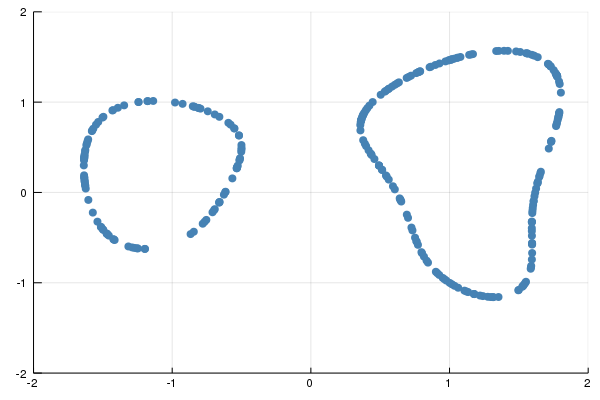
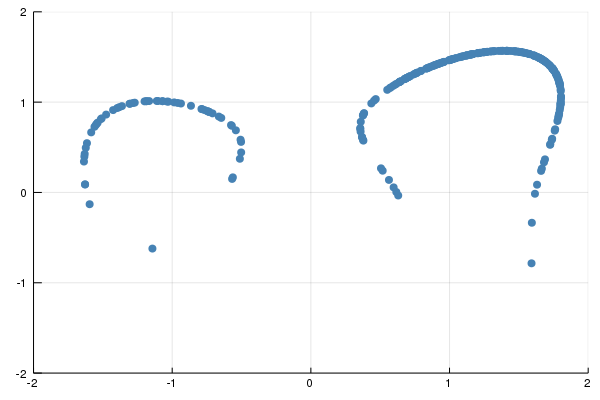
The code can easily be adapted to sample from other densities. For instance, changing to f(x) = exp(2x[2]), K=exp(4) samples from a distribution that gives more weight to points in the upper half plane. Here is a picture.
@Misc{ sampling2025 ,
author = { Paul Breiding },
title = { Sampling a probability distribution on a variety },
howpublished = { \url{ https://www.JuliaHomotopyContinuation.org/examples/sampling/ } },
note = { Accessed: May 5, 2025 }
}