Let two ellipses be centered at points $p_1,p_2$: $$ E_i( r ) = \{x\in \mathbb{R}^2 \mid (x-p_i)^T Q_i^TQ_i(x-p_i) = r^2\}, i=1,2, $$ where $Q_1, Q_2$ are symmetric matrices.
We wish to find the smallest radius $r$ for which $E_1( r )\cap E_2( r )$ is not empty. Let $r^\star$ be the solution for this optimization problem. In Julia we translate this into a polynomial system:
using HomotopyContinuation, LinearAlgebra
# generate the variables
@polyvar Q₁[1:2, 1:2] Q₂[1:2, 1:2] p₁[1:2] p₂[1:2]
@polyvar x[1:2] r
z₁ = x - p₁
z₂ = x - p₂
# initialize the equations for E₁ and E₂
f₁ = (Q₁ * z₁) ⋅ (Q₁ * z₁) - r^2
f₂ = (Q₂ * z₂) ⋅ (Q₂ * z₂) - r^2
# initialize the equation for E₁ and E₂ being tangent
@polyvar λ
g = (Q₁' * Q₁) * z₁ - λ .* (Q₂' * Q₂) * z₂
# gather everything in one system
F = [f₁; f₂; g];
An initial solution is given by two circles, each of radius 1, centered at $(1,0)$ and $(-1,0)$, respectively. Let us track this solution to the system given by
$$p_1 = [3,0], p_2 = [1,2], Q_1 = \begin{pmatrix} 1 & 1\\ 1 & 0 \end{pmatrix}, Q_2 = \begin{pmatrix} 0 & 2 \\ 2 & 1 \end{pmatrix}.$$
That is, the parameters are $p_1, p_2, Q_1, Q_2$ and the variables are $x,r,λ$. Now we track the starting solution towards the target system
julia> params = [vec(Q₁); vec(Q₂); p₁; p₂]
julia> q = [1, 0, 0, 1, 1, 0, 0, 1, 1, 0, -1, 0]
julia> p = [vec([1 1; 1 0]); vec([0 2; 2 1]); [3, 0]; [1, 2]]
julia> solve(F, [[0, 0, 1, -1]], parameters=params, start_parameters=q, target_parameters=p)
Result with 1 solutions
==================================
• 1 non-singular solution (1 real)
• 0 singular solutions (0 real)
• 1 paths tracked
• random seed: 805680
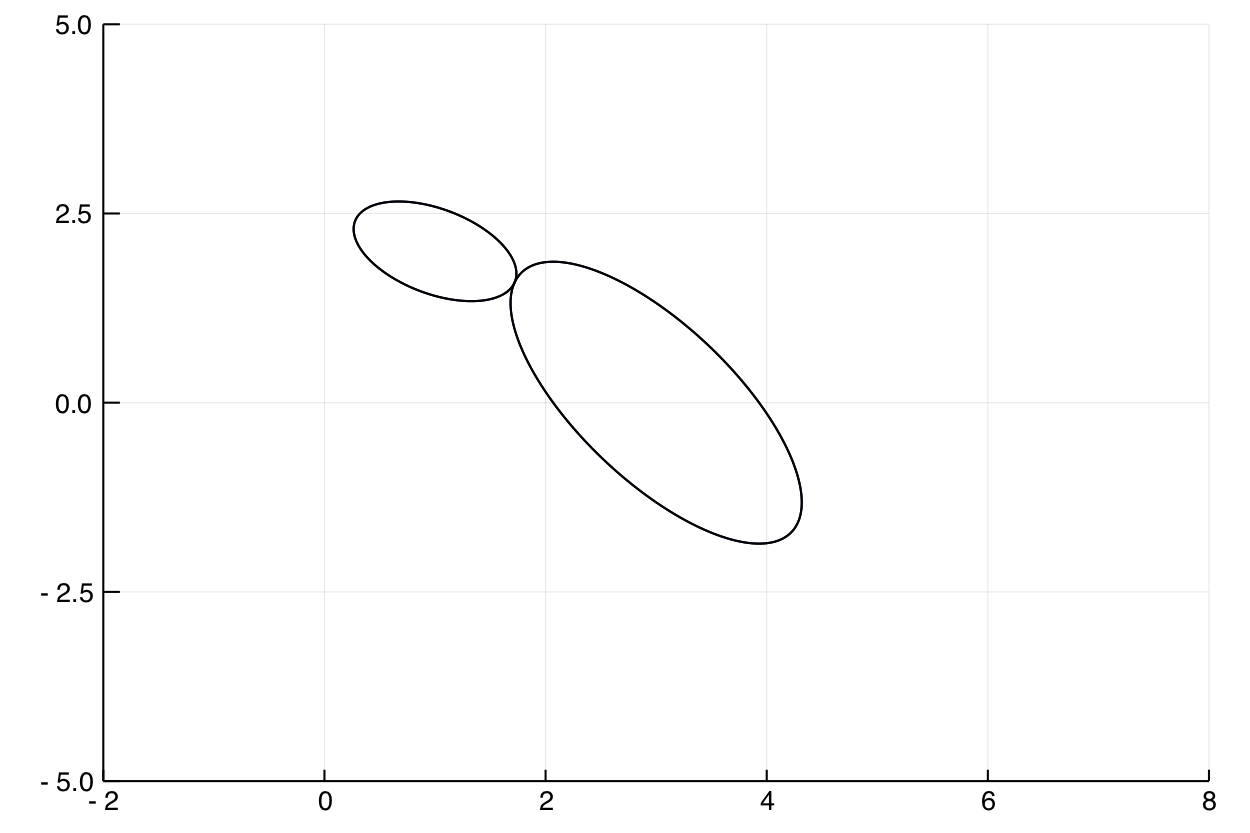
The computation reveals that $r^\star \approx 1.317$. Here is a picture.
@Misc{ ellipses-tangent2023 ,
author = { Paul Breiding },
title = { When do two ellipses meet? },
howpublished = { \url{ https://www.JuliaHomotopyContinuation.org/examples/ellipses-tangent/ } },
note = { Accessed: March 10, 2023 }
}