Curvature of curves in the plane
Consider the problem of computing the point on a (smooth) curve $V\subset \mathbb{R}^n$, where the curvature is maximal. We can use the following formula for curvature at a point $p\in V = \{f(x_1,x_2)=0\}$.
$$\sigma(p) = \frac{v^T H v}{g^\frac{3}{2}}$$
where $v^T \nabla_p f(p) = 0$, and $v^T v=1$, and $H$ is the Hessian of $f$ at $p$, and $g = \nabla_p f(p)^T\nabla_p f(p)$. The conditions for $\sigma(p)$ being maximal on $V$ are thus $v^T \nabla_p \sigma(p)=0$ and $f(p)=0$.
Thus, for maximizing $\sigma$ over
$$V =\{x_1^4 - x_1^2x_2^2 + x_2^4 - 4x_1^2 - 2x_2^2 - x_1 - 4x_2 + 1 = 0\}$$
we use the following code.
using HomotopyContinuation, LinearAlgebra
@var x[1:2]# initialize variables
f = x[1]^4 - x[1]^2*x[2]^2 + x[2]^4 - 4x[1]^2 - 2x[2]^2 - x[1] - 4x[2] + 1
∇ = differentiate(f, x) # the gradient
H = differentiate(∇, x) # the Hessian
g = ∇ ⋅ ∇
v = [-∇[2]; ∇[1]]
h = v' * H * v
dg = differentiate(g, x)
dh = differentiate(h, x)
F = [(g .* dh - ((3/2) * h).* dg) ⋅ v; f]
solve(F)
Result with 56 solutions
========================
• 64 paths tracked
• 56 non-singular solutions (12 real)
• random_seed: 0xa10d5d18
• start_system: :polyhedral
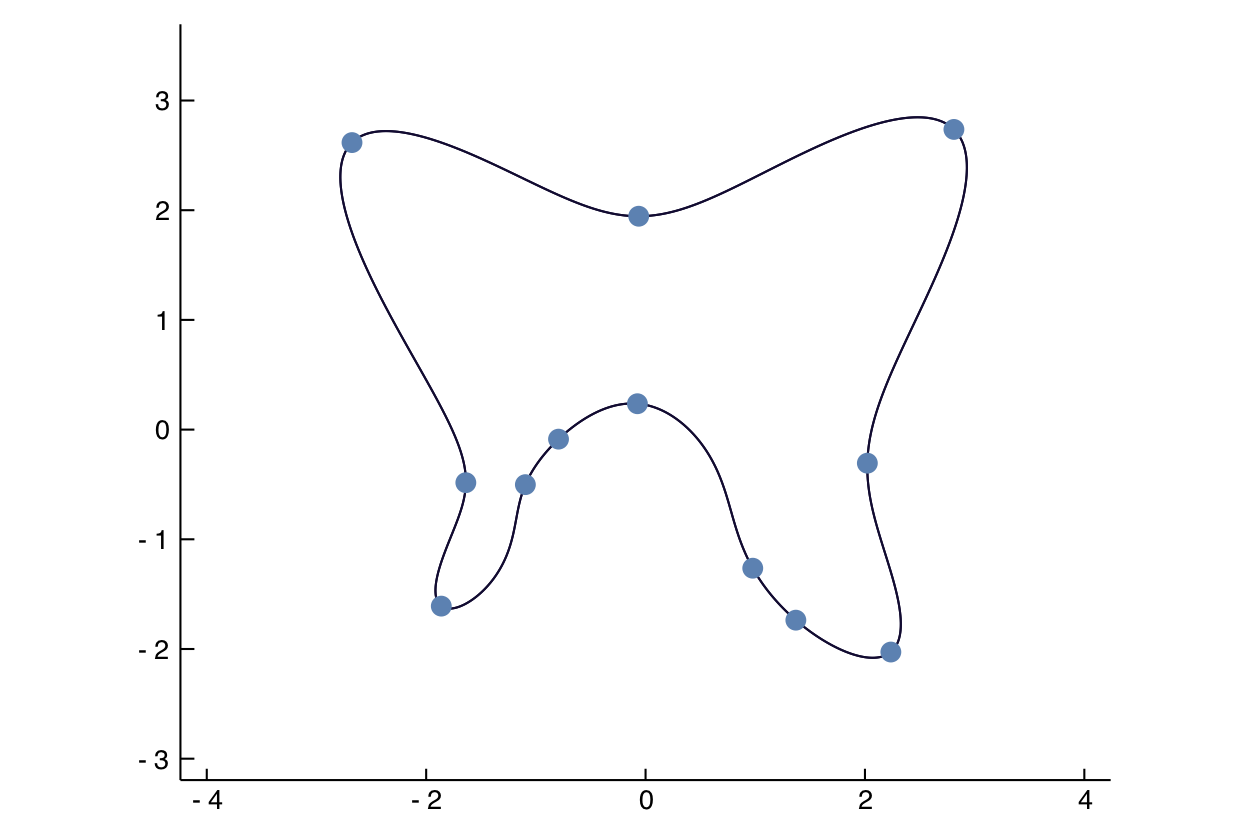
Here is a picture of all solutions.
@Misc{ curvature2023 ,
author = { Paul Breiding },
title = { Curvature of plane curves },
howpublished = { \url{ https://www.JuliaHomotopyContinuation.org/examples/curvature/ } },
note = { Accessed: March 10, 2023 }
}