Consider the problem of computing the point on
$$ V = \{x=(x_1,x_2)^T\in \mathbb{R}^2 : f(x) = 0\}, \text{ for } f(x) = x_1^2 + x_2^2 - (x_1^2 + x_2^2 + x_2)^2, $$
which minimizes the distance to the point $u₀ = (-3,-2)$. The situation looks like this:
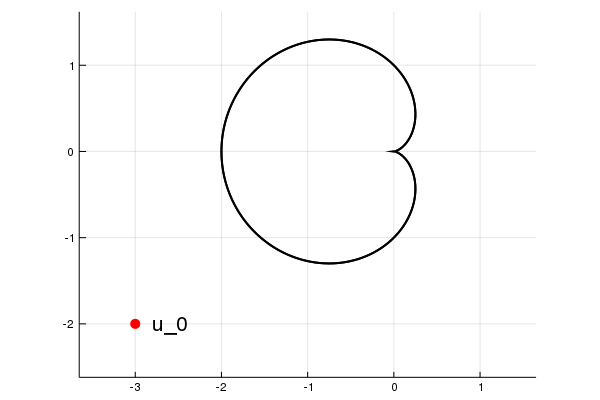
The minimizer $x^\star$ is a solution to the system
$$ F_u = \begin{bmatrix}\det(\begin{bmatrix}x-u & \nabla_x(f)\end{bmatrix})\\ f(x)\end{bmatrix} =0, $$
where $\nabla_x(f)$ is the gradient of $f$ at $x$. Let's set up this system in Julia.
using HomotopyContinuation, LinearAlgebra
u₀ = [-2; -1]
@var x[1:2]
f = x[1]^2 + x[2]^2 - (x[1]^2 + x[2]^2 + x[1])^2
∇ = differentiate(f, x)
F = [det([x-u₀ ∇]); f]
Now, $x^\star$ is a zero of F, which has total degree equal to 12. However, the actual number of solutions is only 3 as was shown in this article. For avoiding computing all 12 paths, we use monodromy instead of total degree tracking.
An initial solution to F is $x_0=(0,1)^T$. Let's use this initial solution for monodromy:
using HomotopyContinuation
x₀ = [0; 1]
@var u[1:2]
F_u = [det([x-u ∇]); f]
monodromy_solve(F_u, [x₀], u₀, parameters = u)
MonodromyResult
==================================
• 3 solutions (3 real)
• return code → heuristic_stop
• 111 tracked paths
We get the three solutions. The following picture shows them:
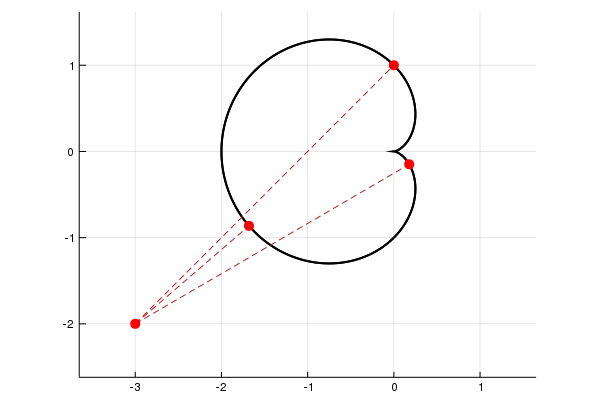
The minimizer is $x^\star \approx (-1.68, -0.86)^T$.
Cite this example:
@Misc{ critical-points2023 ,
author = { Paul Breiding, Sascha Timme },
title = { The point on a variety that minimizes the distance to a given point },
howpublished = { \url{ https://www.JuliaHomotopyContinuation.org/examples/critical-points/ } },
note = { Accessed: March 10, 2023 }
}