Consider the problem of computing all circles that are tangent to 3 conics $C_1,C_2,C_3 \subset \mathbb{R}^2$. For instance, the following picture shows 14 circles that are tangent to
$$C_1 = \{y=-x^2+2x+5\},$$
$$C_2 = \{y = 2x^2+5x-8\},$$
$$C_3 = \{y = 8x^2-3x-2\}.$$
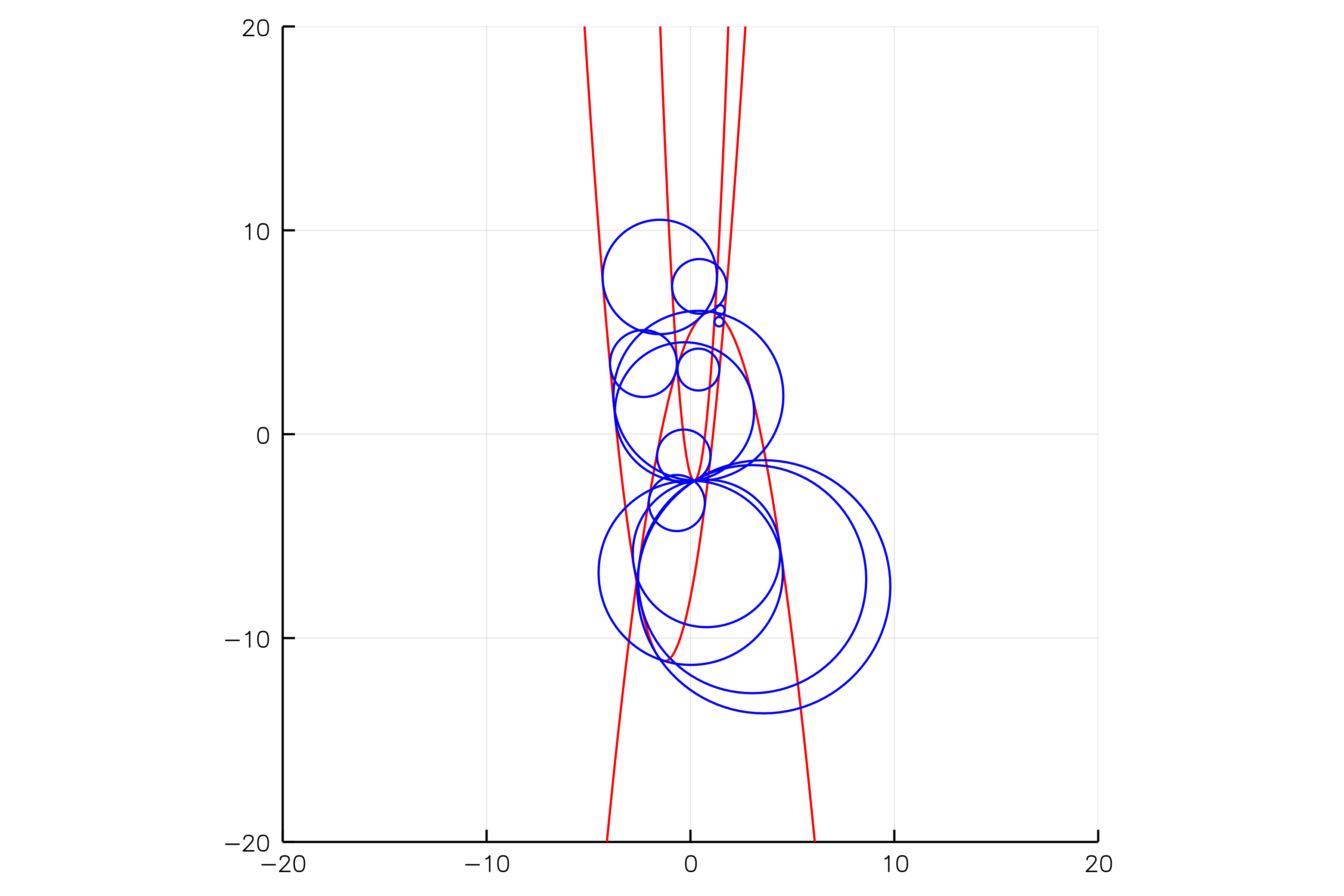
Emiris and Tzoumas write that there are 184 complex circles that are tangent to 3 general conics. This means, that there are 184 complex solutions $(a_1,a_2,r)$ such that there exists some $(x,y)\in\mathbb{C}^2$ with
-
$(x-a_1)^2 + (y-a_2)^2 = r$,
-
$(x,y)\in C_i, 1\leq i\leq 3$, and
-
$(\overline{x}-\overline{a_1}, \overline{y}-\overline{a_2})$ spans the normal space of $C_i$ at $(x,y)$ for $1\leq i\leq 3$.
How many real solutions can this system have? Only real solutions give circles in the real plane.
Here is code to generate the above system for random coefficients of the conics.
using HomotopyContinuation, DynamicPolynomials, LinearAlgebra
@var a[1:2] r #variables for the circle center and radius
@var x y #variables of the circle
@var B[1:3,1:3] #coefficients of the conics
@var v[1:2, 1:3] #variables of the 3 points at which the circle is tangent
circle = ([x; y] - a) ⋅ ([x; y] - a) - r
conic = [x; y; 1] ⋅ (B * [x; y; 1]);
tangential_condition = det([differentiate(circle, [x, y]) differentiate(conic, [x, y])])
conditions = [circle; conic; tangential_condition]
#define coefficients of the three conics
C1 = randn(3,3)
C2 = randn(3,3)
C3 = randn(3,3)
#Plug in the variables of the 3 points
#and coefficients of the 3 conics
F = [
f([x; y; a; r; vec(B)] => [v[:,i]; a; r; vec(C)])
for f in conditions
for (i,C) in enumerate([C1, C2, C3])
]
solve(F)
I get the following answer.
Result with 184 solutions
=========================
• 256 paths tracked
• 184 non-singular solutions (26 real)
• random_seed: 0xfcbca7ff
• start_system: :polyhedral
And here is the code for $C_1$, $C_2$ and $C_3$ above.
C1 = [-1 0 1; 0 0 -0.5; 1 -0.5 5]
C2 = [2 0 2.5; 0 0 -0.5; 2.5 -0.5 -8]
C3 = [8 0 -1.5; 0 0 -0.5; -1.5 -0.5 -2]
F = [
f([x; y; a; r; vec(B)] => [v[:,i]; a; r; vec(C)])
for f in conditions
for (i,C) in enumerate([C1, C2, C3])
]
solve(F)
Result with 62 solutions
========================
• 108 paths tracked
• 62 non-singular solutions (14 real)
• random_seed: 0xaf5b2b3b
• start_system: :polyhedral
@Misc{ circles-conics2025 ,
author = { Paul Breiding },
title = { The number of circles that are tangent to 3 given conics },
howpublished = { \url{ https://www.JuliaHomotopyContinuation.org/examples/circles-conics/ } },
note = { Accessed: May 5, 2025 }
}