A conic in the plane $\mathbb{R}^2$ is the zero set of a quadratic polynomial in two variables:

$$ a_1 x^2 + a_2 xy + a_3 y^2 + a_4 x + a_5 y + a_6 .$$

Geometrically, a conic can be either a circle, an ellipse, a hyperbola, a parabola or a union of two lines. The last case is a degenerate conic. Double lines are allowed.

A classic problem in enumerative geometry is Steiner's conic problem which asks:

*How many conics are tangent to five given conics?*

Here is an example of Steiner's problem:

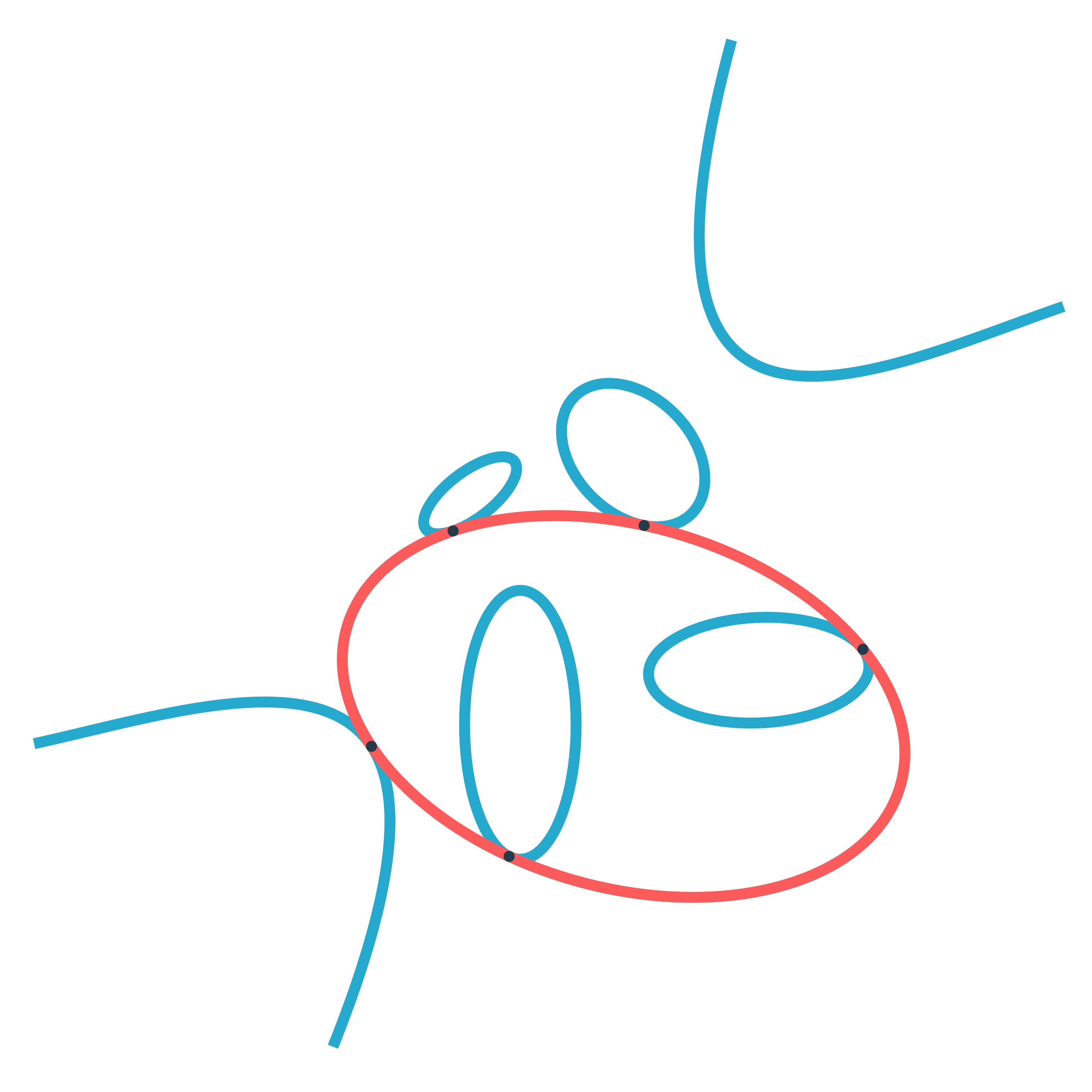
Steiner claimed in 1848 that there are at most 7776 conics tangent to 5 given conics. He phrased his problem as that of solving five equations of degree six on the 5-dimensional projective space $\mathbb{P}^5$. Using Bézout's Theorem he argued that the equations coming from this question have $6^5 = 7776$ solutions over the complex numbers. However, this number over counts because there is a Veronese surface of extraneous solutions, namely the conics that are squares of linear forms, i.e., double lines.

The correct count of non-degenerate conics is 3264. This was shown in 1859 by Jonquières and independently in 1864 by Chasles. The number 3264 appears prominently in the book 3264 and all that by Eisenbud and Harris.

A delightful introduction to Steiner's problem was given by Bashelor, Ksir and Traves. Ronga, Tognoli and Vust and Sottile showed how to choose 5 real conics such that all 3264 complex solutions are real. Although their proofs starts with an explicit construction, it is not constructive.

Using methods from numerical algebraic geometry we adapted the proposed construction to find an explicit instance for which there are 3264 real conics. We use numerical homotopy continuation to compute the 3264 conics. Smale's $\alpha$-theory provides a way to give a mathematical proof that we found 3264 real conics; the keyword is alphaCertified. The computational proof can be downloaded here.

An illustration of the arrangement is shown below.

It looks like the arrangement consists of 5 blue lines, rather than 5 blue conics. The next picture clarifies the situation.

More details on the geometry of this particular conic arrangement can be found in the article 3264 conics in a Second.

Cite this example:

@Misc{ 32642024 ,
    author =  { Paul Breiding, Bernd Sturmfels and Sascha Timme },
    title = { 3264 conics tangent to five conics },
    howpublished = { \url{ https://www.JuliaHomotopyContinuation.org/examples/3264/ } },
    note = { Accessed: November 26, 2024 }
}

Published by Paul Breiding, Bernd Sturmfels and Sascha Timme 12 Feb, 2019